1) Differentiering: En Grundläggande Guide
- Innan vi kan utforska kalkylens värld måste vi förstå konceptet differentiering.
- Differentiering hjälper oss att hitta tangentlinjen till en kurva vid en specifik punkt.
- En tangentlinje är en linje som bara berör kurvan i en enda punkt.
- För att hitta tangentlinjen behöver vi kunna beräkna dess lutning.
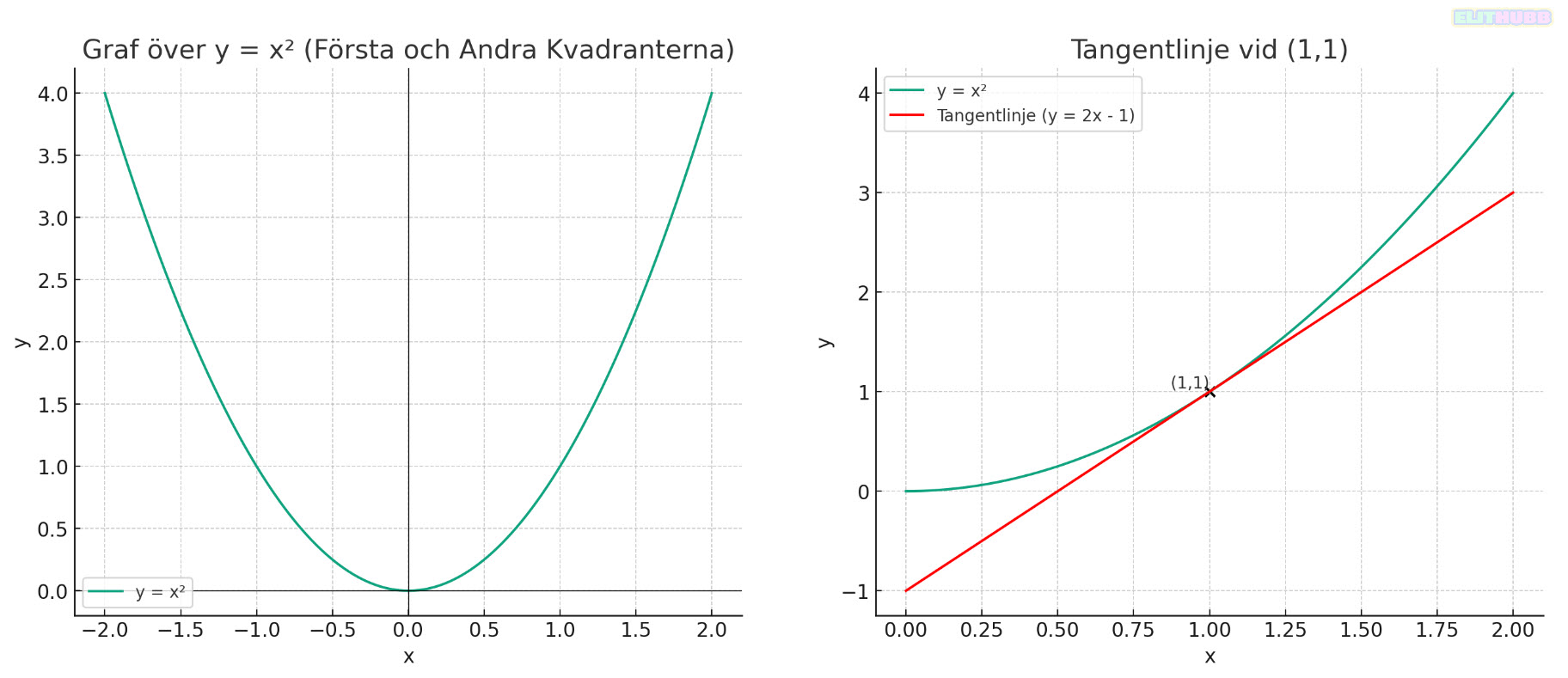
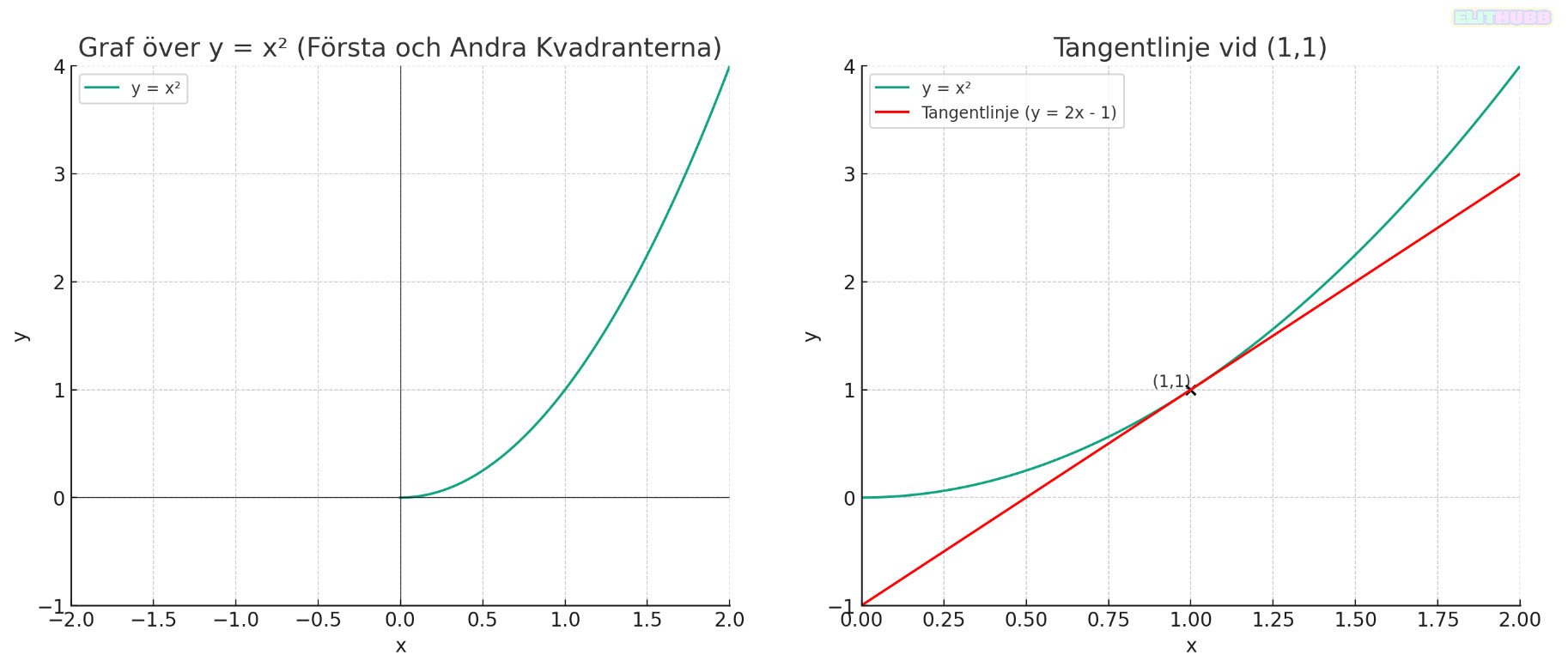
Låt oss använda ett exempel med den enkla parabeln y = x² för att förklara differentiering.
Steg 1: Välj en punkt på kurvan
- Låt oss välja punkten (1, 1) på kurvan y = x². Vi vet att denna punkt ligger på kurvan eftersom 1 upphöjt till 2 är 1.
Steg 2: Beräkna lutningen för en sekantlinje
- För att beräkna lutningen för tangentlinjen behöver vi först skapa en sekantlinje genom att välja en annan punkt på kurvan.
- Låt oss välja en punkt med koordinaterna (x, x²).
- Lutningen för sekantlinjen beräknas med hjälp av formeln:
- Lutning = (y2 – y1) / (x2 – x1)
- I vårt fall blir det: (x² – 1) / (x – 1).
Steg 3: Använd olika punkter närmare den ursprungliga punkten
- Nu kan vi välja olika värden för x och se hur lutningen ändras när den andra punkten närmar sig (1, 1).
- Ju närmare vi kommer, desto mer liknar sekantlinjen tangentlinjen.
- Om vi väljer x = 2 får vi en lutning på 3, och om vi väljer x = 1.5 får vi en lutning på 2.5.
- Genom att fortsätta närma oss punkten (1, 1) från båda hållen, ser vi att lutningen närmar sig 2.
- Här är en tabell som visar punkten x och lutningen m för både x-värden närmare den ursprungliga punkten (1, 1) från båda hållen, dvs. när x närmar sig 1 från både höger och vänster:
| x-värde | Lutning (m) |
|---|---|
| 2 (punkter som är större än 1) | 3 |
| 1.5 | 2.5 |
| 1.2 | 2.2 |
| 1.1 | 2.1 |
| 1.05 | 2.05 |
| 1.01 | 2.01 |
| 1.001 | 2.001 |
| 1 (ursprunglig punkt) | 2 (tangentlinjens lutning) |
| 0.999 | 1.999 |
| 0.99 | 1.99 |
| 0.95 | 1.95 |
| 0.9 | 1.9 |
| 0.8 | 1.8 |
| 0.5 | 1.5 |
| 0.2 | 1.2 |
| 0 (punkter som är mindre än 1) | 1 (tangentlinjens lutning) |
- Tabellen visar hur lutningen m ändras när x-värdet närmar sig 1 från höger och vänster sida av den ursprungliga punkten (1, 1).
- Lutningen närmar sig 2 från båda hållen, vilket bekräftar att tangentlinjen har en lutning på 2 vid den punkten.
Steg 4: Beräkna tangentlinjens ekvation
- Om lutningen är 2, kan vi använda ekvationen för en linje, y = mx + b, där m är lutningen och (1, 1) är vår punkt:
- 1 = 2 * 1 + b
- Vi löser för b
- b = -1
- Genom att lösa detta ekvationssystem får vi b = -1. Därför blir ekvationen för tangentlinjen:
- y = 2x – 1
- Lutningen (m) är 2 eller 2/1 (2 över 1)
- Vilket betyder att vi går upp 2 enheter och sedan går vi en enhet åt höger
- Skärningspunkten (b) vid y-axeln är -1
- Genom att hitta lutningen för tangentlinjen har vi genomfört differentiering och förstått något om hastigheten med vilken funktionen ändras vid den specifika punkten (1, 1).
- Grafen visar parabeln y = x² och dess tangentlinje vid punkten (1,1). Tangentlinjen är y = 2x – 1, vilket visar att vid punkten (1,1) har parabeln en lutning av 2.
- Detta illustrerar processen av differentiering för att hitta tangentlinjens lutning vid en specifik punkt på kurvan.
- Genom att se på grafen kan vi förstå hur funktionen förändras och att funktionen ökar med en hastighet av 2 enheter per enhet längs x-axeln vid den punkten.
Differentiering och Förändringshastighet
- Differentiering hjälper oss också att förstå förändringshastigheten i en funktion. Om vi vet att tangentlinjen har en lutning av 2 vid punkten (1, 1), innebär det att funktionen ökar med en hastighet av 2 enheter per enhet längs x-axeln vid den punkten.
- Detta ger oss en annan synvinkel på differentiering – den hjälper oss att förstå hur snabbt en funktion förändras vid olika punkter på kurvan.
- Genom att behärska differentiering kan vi lösa en mängd matematiska problem och förstå komplexa kurvor och deras egenskaper på djupet.
- Det är ett kraftfullt verktyg inom matematik och har många tillämpningar inom vetenskap och teknik.